Kaniner och spiraler

 FÖRSTA SIDAN

Det gåtfulla och oväntade sambandet mellan kottar, solrosor och ett matematiskt problem från 1200-talet som till sist visar sig innesluta såväl kronärtskockor som ananas och en och annan kaktus.

Gran- och tallkotte

Kottefjällen bildar spiralformer

Den rödmarkerade spiralen går snabbt mot toppen, den som är markerad blå snirklar sig en längre väg.

Och nu till något helt annat. I början av 1200-talet var inte vårt moderna siffersystem, positionssytemet, allmänt känt (man skrev ännu talen med det latinska systemet där t.ex. 2013 skrivs i formen MMXIII). Matematikern Fibonacci hade lärt sig av de arabiska matematikerna (som hämtat systemet från Indien) och skrev i sin bok Liber abaci (1202) att "de nio indiska siffrorna är: 9 8 7 6 5 4 3 2 1 och med dessa nio siffror, och med tecknet 0 ... kan alla tal skrivas". I samma skrift ställde han upp ett kaninproblem med föjande regler:

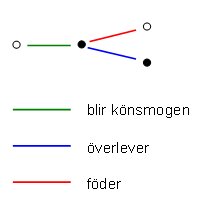
1. Från början har man ett kaninpar
2. Varje månad föder ett kaninpar ett nytt kaninpar
3. Efter en månad kan det nya kaninparet
    föda ytterligare ett par
4. Inga kaniner dör eller tillkommer på annat sätt

Man har alltså ett par till att börja med och som efter en månad föder ytterligare ett par. Så här såg det ut efter två månader (ofylld ring är ett ofruktsamt par, fylld ring representerar ett par som kan föda en ny generation).

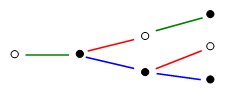
Efter ytterligare en månad föder det nya paret ett nytt par samtidigt som det ursprungliga paret föder ett nytt par. Antalet par är nu 3.

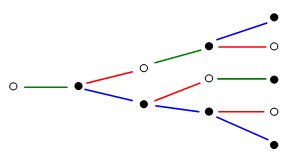
En månad senare är antalet par fem

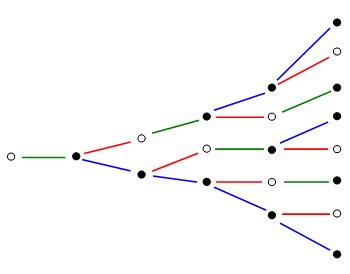
Och ännu en månad senare finns åtta kaninpar.

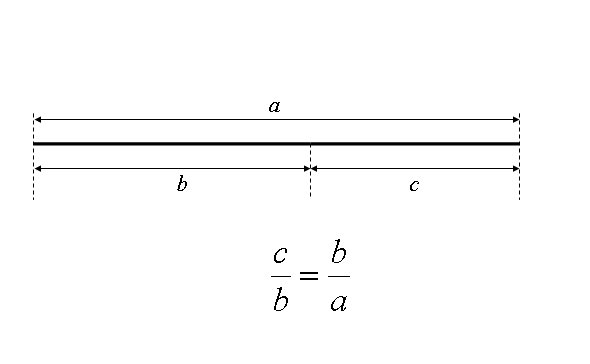
Man får en talserie: 1 1 2 3 5 8 ... Talserien kallas "fibonaccitalen" och man får nästa tal i serien genom att lägga samman de två föregående:

1   1   2   3   5   8   13   21   34   55   89   144   233 ...

Den här talserien har en oväntad egenskap. Om man dividerar två på varandra följande tal med varandra får man en kvot som kommer närmare och närmare det gyllene snittet, 1,6180339887799 (eller 0,6180339887799 om man dividerar åt den andra hållet). Proportionerna är ungefär 8:5 vilket är svenska flaggans proportioner och ungefär samma proportioner som hos ett kreditkort. Bland annat.

Att dela en sträcka i gyllene snittet innebär att den kortare delen ska förhålla sig till den längre som den längre förhåller sig till hela sträckan:

En vacker animerad kortfilm som illustrerar fibonaccitalen och det gyllene snittet finner du här.
Om du är intresserad av att läsa om bakgrunden till filmen finns mer information här.

Men låt oss återgå till kottarna och spiralerna. Så här lindar sig barren runt en ung grangren, en brant signing och en flackare:

På en lite grövre stam har barren lossnat och lämnat ärr. Så här sitter de ordnade runt hela stammen.

13 spiraler av det långdragna slaget (blå) och 21 snabba (röda). Tal nummer sju och åtta i fibonacciserien.

Här är ett par tallkottar sedda "bakifrån", den ena med spiralerna markerade.

På den vänstra kotten är det 8 "långdragna" (blå) spiraler och 13 "snabba" (röda) spiraler. Det är tal nummer sex och sju i fobonacciserien.

Den här typen av dubbelspiraler finns också bland annat hos korgblommiga växter, till exempel hos prästkrage och solros.

Hos de här prästkragarna är inte spiralerna särskilt tydliga – lite kaosartade. Särskilt svårt att hitta spiralerna är när inte centrum är klart markerat som på den vänstra bilden.

Men här syns prästkragens spiralformer tydligt:

(bilderna är publicerade med upphovsmannens tillstånd)

Det är samma bild i båda fallen, den understa har spiralformerna markerade. Det är 21 "långdragna" (blå) och 34 "snabba" (röda). Tal nummer 8 och 9 i fibonacciserien.

Chrysantemum saknar ofta ett uttalat centrum och därför blir spiralformerna bara antydda och man finner ett mönster som verkar ofullgånget. Spiralformerna finns där, men är avbrutna på några ställen.

Ytterligare några exempel på geometrin hos korgblommiga växter:

Solros 21-34

Solros 21-34

Solros 34-55

Gerbera 21-34

Det är inte bara hos kottar, granstammar och blommorna hos korgblommiga växter man hittar dessa "fibonaccispiraler". Kronärtskockan (också en krogblommig växt) i följande bild har holkfjällen ordnade i 5 långsamma och 8 snabba spiraler.

Ananas i följande exempel visar två typer av spiralbildningar. Den ena, på jordstammen – den skenfrukt som vi äter som ananas – har 8 långsamma och 13 snabba spiraler medan bladrosetten har 5 långsamma och 8 snabba.

Dessutom är riktningarna hos bladrosettens spiraler spegelvända mot spiralernas riktningar på jordstammen.

Kaktus 8-13

Det här "fibionacciska" sambandet finns inte överallt. Ett exempel på en annan ordning är lupinerna där spiralerna är 7, 8 eller 9 eller i kombinationer 7,8; 7,7; 8,8 eller 8,9 eller andra varianter (n,n eller n,n+1). Man finner en mer eller mindre rak linje upp mot toppen.

Om man söker efter bilder på fraktaler på internet dyker det upp flera bilder av blomkål Romanesca som med sin strama form visar ett fraktalmönster, dvs. en geometrisk likhet som sträcker sig från helheten ner till detaljnivå. Också här syns de dubbla spiralerna tydligt.

Visst är det väl lite märkligt att det finns ett så starkt samband mellan ett kaninproblem och växternas geometri!

Bosse Lundberg